RL— Introduction to Deep Reinforcement Learning
Deep reinforcement learning is about taking the best actions from what we see and hear. Unfortunately, reinforcement learning RL has a high barrier in learning the concepts and the lingos. In this article, we will cover deep RL with an overview of the general landscape. Yet, we will not shy away from equations and lingos. They provide the basics in understanding the concepts deeper. We will not appeal to you that it only takes 20 lines of code to tackle an RL problem. The official answer should be one! But we will try hard to make it approachable.
In most AI topics, we create mathematical frameworks to tackle problems. For RL, the answer is the Markov Decision Process (MDP). It sounds complicated but it produces an easy framework to model a complex problem. An agent (e.g. a human) observes the environment and takes actions. Rewards are given out but they may be infrequent and delayed. Very often, the long-delayed rewards make it extremely hard to untangle the information and traceback what sequence of actions contributed to the rewards.
Markov decision process (MDP) composes of:


State in MDP can be represented as raw images.

Or for robotic controls, we use sensors to measure the joint angles, velocity, and the end-effector pose:

- An action can be a move in a chess game or moving a robotic arm or a joystick.
- For a GO game, the reward is very sparse: 1 if we win or -1 if we lose. Sometimes, we get rewards more frequently. In the Atari Seaquest game, we score whenever we hit the sharks.
- The discount factor discounts future rewards if it is smaller than one. Money earned in the future often has a smaller current value, and we may need it for a purely technical reason to converge the solution better.

- We can rollout actions forever or limit the experience to N time steps. This is called the horizon.
The transition function is the system dynamics. It predicts the next state after taking action. It is called the model which plays a major role when we discuss Model-based RL later.
Convention
The concepts in RL come from many research fields including the control theory. Different notations are used in different contexts. Unfortunately, this is quite unavoidable when reading RL materials. So, let’s get this out first before any confusion. The state can be written as s or x, and action as a or u. Action is the same as control. We can maximize the rewards or minimizes the costs which are simply negative of each other. Notations can be in upper or lower case.

Policy
In RL, our focus is finding an optimal policy. A policy tells us how to act from a particular state.

Like the weights in Deep Learning methods, this policy can be parameterized by θ,

and we want to find a policy that makes the most rewarding decisions:

In real life, nothing is absolute. So our policy can be deterministic or stochastic. For stochastic, the policy outputs a probability distribution instead.


Finally, let’s put our objective together. In RL, we want to find a sequence of actions that maximize expected rewards or minimize cost.

But there are many ways to solve the problem. For example, we can
- Analyze how good to reach a certain state or take a specific action (i.e. Value-learning),
- Use the model to find actions that have the maximum rewards (model-based learning), or
- Derive a policy directly to maximize rewards (policy gradient).
We will go through all these approaches shortly.
Notation
But, in case you want further elaboration for the terms and notation in RL first, this table should help.

Model-based RL
Intuitively, if we know the rule of the game and how much it costs for every move, we can find the actions that minimize the cost. The model p (the system dynamics) predicts the next state after taking an action. Mathematically, it is formulated as a probability distribution. In this article, the model can be written as p or f.

Let’s demonstrate the idea of a model with a cart-pole example. p models the angle of the pole after taking action.


Here is the probability distribution output for θ in the next time step for the example above.

This model describes the law of Physics. But a model can be just the rule of a chess game. The core idea of Model-based RL is using the model and the cost function to locate the optimal path of actions (to be exact — a trajectory of states and actions).

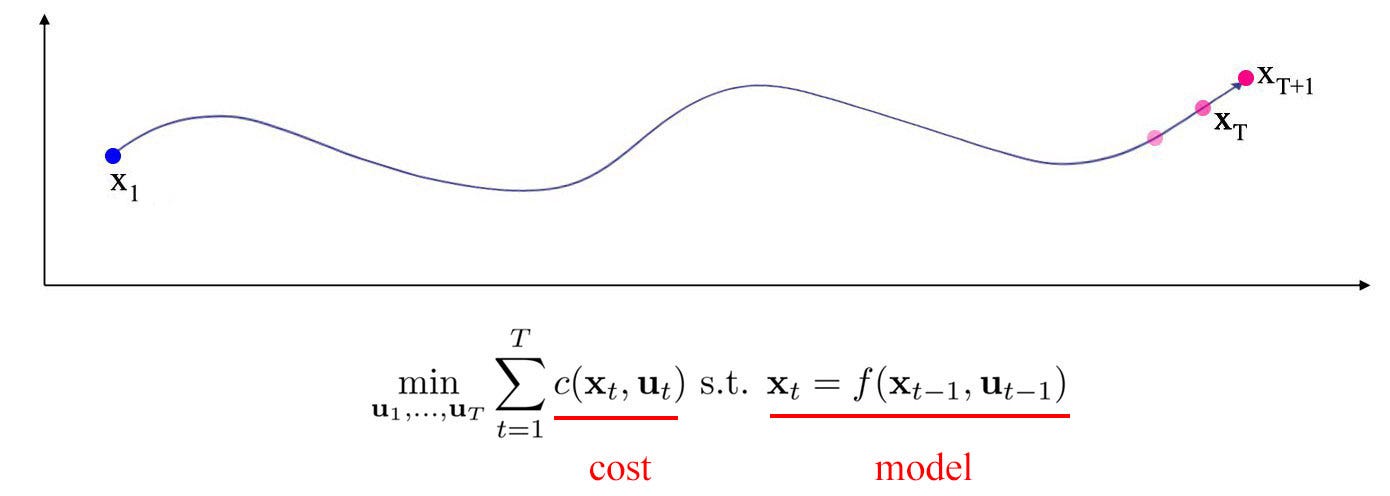
Let’s get into another example. In the GO game, the model is the rule of the game. According to this rule, we search the possible moves and find the actions to win the game. Of course, the search space is too large and we need to search smarter.
In model-based RL, we use the model and cost function to find an optimal trajectory of states and actions (optimal control).
Sometimes, we may not know the models. But this does not exclude us from learning them. Indeed, we can use deep learning to model complex motions from sample trajectories or approximate them locally.
The video below is a nice demonstration of performing tasks by a robot using Model-based RL. Instead of programming the robot arm directly, the robot is trained for 20 minutes to learn each task, mostly by itself. Once it is done, the robot should handle situations that have not trained before. We can move around the objects or change the grasp of the hammer, the robot should manage to complete the task successfully.
The tasks sound pretty simple. But they are not easy to solve. We often make approximations to make it easier. For example, we approximate the system dynamics to be linear and the cost function to be a quadratic equation.


Then we find the actions that minimize the cost while obeying the model.

There are known optimization methods like LQR to solve this kind of objective. To move to non-linear system dynamics, we can apply iLQR which use LQR iteratively to find the optimal solution similar to Newton’s optimization. All these methods are complex and computationally intense. You can find the details in here. But for our context, we just need to know that given a cost function and a model, we can find the corresponding optimal actions.
Model-based RL has a strong competitive edge over other RL methods because it is sample efficiency. Many models can be approximated locally with fewer samples and trajectory planning requires no further samples. If physical simulation takes time, the saving is significant. Therefore, it is popular in robotic control. With other RL methods, the same training may take weeks.
Let’s detail the process a little bit more. The following is the MPC (Model Predictive Control) which runs a random or an educated policy to explore space to fit the model. Then, in step 3, we use iLQR to plan the optimal controls. But we only execute the first action in the plan. We observe the state again and replan the trajectory. This allows us to take corrective actions if needed.

The following figure summarizes the flow. We observe the environments and extract the states. We fit the model and use a trajectory optimization method to plan our path which composes of actions required at each time step.

Value learning
Next, we go to another major RL method called Value Learning. In playing a GO game, it is very hard to plan the next winning move even the rule of the game is well understood. The exponential growth of possibilities makes it too hard to be solved. When the GO champions play the GO game, they evaluate how good a move is and how good to reach a certain board position. Assume we have a cheat sheet scoring every state:

We can simply look at the cheat sheet and find what is the next most rewarding state and take the corresponding action.
Value function V(s) measures the expected discounted rewards for a state under a policy. Intuitively, it measures the total rewards that you get from a particular state following a specific policy.

In our cart-pole example, we can use the pole stay-up time to measure the rewards. Below, there is a better chance to maintain the pole upright for the state s1 than s2 (better to be in the position on the left below than the right). For most policies, the state on the left is likely to have a higher value function.

So how to find out V? One method is the Monte Carlo method. We run the policy and play out the whole episode until the end to observe the total rewards. For example, we time how long the pole stays up. Then we have multiple Monte Carlo rollouts and we average the results for V.
There are a few ways to find the corresponding optimal policy. In policy evaluation, we can start with a random policy and evaluate how good each state is. After many iterations, we use V(s) to decide the next best state. Then, we use the model to determine the action that leads us there. For the GO game, this is simple since the rule of the game is known.

Alternatively, after each policy evaluation, we improve the policy based on the value function. We continue the evaluation and refinement. Eventually, we will reach the optimal policy. This is called policy iteration.

But there is a problem if we do not have the model. We do not know what action can take us to the target state.
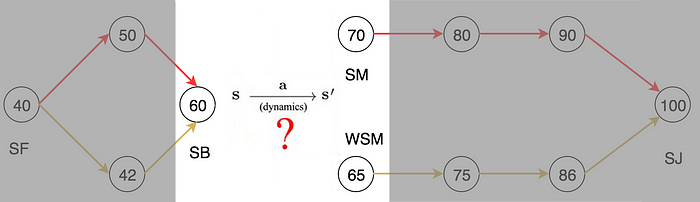
Value function is not a model-free method. We need a model to make decisions. But as an important footnote, even when the model is unknown, value function is still helpful in complementing other RL methods that do not need a model.
Value iteration with Dynamic programming
Other than the Monte Carlo method, we can use dynamic programming to compute V. We take an action, observe the reward and compute it with the V-value of the next state:

The exact formula should be:

If the model is unknown, we compute V by sampling. We execute the action and observe the reward and the next state instead.
Function fitting
However, maintain V for every state is not feasible for many problems. To solve that, we use supervised learning to train a deep network that approximates V.
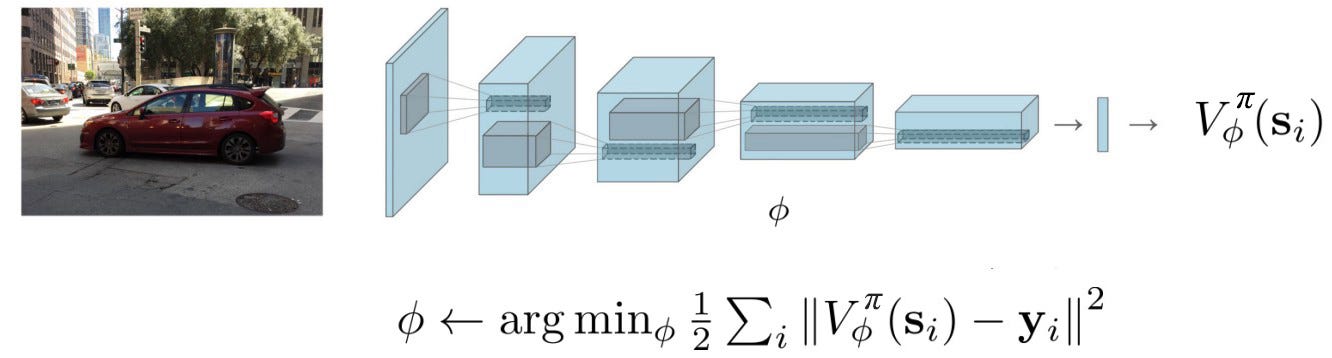
y above is the target value and we can use the Monte Carlo method to compute it.

Otherwise, we can apply the dynamic programming concept and use a one-step lookahead. This is called Temporal Difference TD.

We take a single action and use the observed reward and the V value for the next state to compute V(s).

The Monte Carlo method is accurate. But for a stochastic policy or a stochastic model, every run may have different results. So the variance is high. TD considers far fewer actions to update its value. So the variance is low. But at least in early training, the bias is very high. High bias gives wrong results but high variance makes the model very hard to converge. In practice, we can combine the Monte Carlo and TD with different k-step lookahead to form the target. This balances the bias and the variance which can stabilize the training.
Action-value function
So can we use the value learning concept without a model? Yes, we can avoid the model by scoring an action instead of a state. Action-value function Q(s, a) measures the expected discounted rewards of taking an action. The tradeoff is we have more data to track. For each state, if we can take k actions, there will be k Q-values.

For optimal results, we take the action with the highest Q-value.

As shown, we do not need a model to find the optimal action. Hence, Action-value learning is model-free. Which acton below has a higher Q-value? Intuitively, moving left at the state below should have a higher value than moving right.

In deep learning, gradient descent works better when features are zero-centered. Intuitively, in RL, the absolute rewards may not be as important as how well an action does compare with the average action. That is the concept of the advantage function A. In many RL methods, we use A instead of Q.

where A is the expected rewards over the average actions. To recap, here are all the definitions:



Q-learning
So how can we learn the Q-value? One of the most popular methods is Q-learning with the following steps:
- We sample an action.
- We observed the reward and the next state.
- We take the action with the highest Q.

Then we apply the dynamic programming again to compute the Q-value function iteratively:

Here is the algorithm of Q-learning with function fitting. Step 2 below reduces the variance by using Temporal Difference. This also improves the sample efficiency comparing with the Monte Carlo method which takes samples until the end of the episode.

Exploration is very important in RL. Without exploration, you will never know what is better ahead. But if it is overdone, we are wasting time. In Q-learning, we have an exploration policy, like epsilon-greedy, to select the action taken in step 1. We pick the action with the highest Q value but yet we allow a small chance of selecting other random actions. Q is initialized with zero. Hence, there is no specific action standing out in early training. As the training progress, more promising actions are selected and the training shift from exploration to exploitation.
Deep Q-network DQN
Q-learning is unfortunately not very stable with deep learning. In this section, we will finally put all things together and introduce the DQN which beats the human in playing some of the Atari Games by accessing the image frames only.

DQN is the poster child for Q-learning using a deep network to approximate Q. We use supervised learning to fit the Q-value function. We want to duplicate the success of supervised learning but RL is different. In deep learning, we randomize the input samples so the input class is quite balanced and pretty stable across training batches. In RL, we search better as we explore more. So the input space and actions we searched are constantly changing. In addition, as we know better, we update the target value of Q. That is bad news. Both the input and output are under frequent changes.

This makes it very hard to learn the Q-value approximator. DQN introduces experience replay and target network to slow down the changes so we can learn Q gradually. Experience replay stores the last million of state-action-reward in a replay buffer. We train Q with batches of random samples from this buffer. Therefore, the training samples are randomized and behave closer to the supervised learning in Deep Learning.
In addition, we have two networks for storing the values of Q. One is constantly updated while the second one, the target network, is synchronized from the first network once a while. We use the target network to retrieve the Q value such that the changes for the target value are less volatile. Here is the objective for those interested. D is the replay buffer and θ- is the target network.

DQN allows us to use value learning to solve RL methods in a more stable training environment.
Policy-Gradient
So far we have covered two major RL methods: model-based and value learning. Model-based RL uses the model and the cost function to find the optimal path. Value learning uses V or Q value to derive the optimal policy. Next, we will cover the third major RL method, also one of the popular ones in RL. The Policy Gradient method focuses on the policy.

Many of our actions, in particular with human motor controls, are very intuitive. We observe and act rather than plan it thoroughly or take samples for maximum returns.

In the cart-pole example, we may not know the physics but when the pole falls to the left, our experience tells us to move left. Determining actions based on observations can be much easier than understanding a model.

This type of RL method is policy-based which we model a policy parameterized by θ directly.
The concept for Policy Gradient is very simple. For actions with better rewards, we make it more likely to happen (or vice versa). The policy gradient is computed as:

We use this gradient to update the policy using gradient ascent. i.e. we change the policy in the direction with the steepest reward increase.

Let’s look at the policy gradient closely. The one underlines in red above is the maximum likelihood. It measures the likelihood of an action under a specific policy. As we multiply it with the advantage function, we change the policy to favor actions with rewards greater than the average action. Or vice versa, we reduce the chance if it is not better off.
But we need to be very careful in making such policy change. The gradient method is a first-order derivative method. It is not too accurate if the reward function has steep curvature. If our policy change is too aggressive, the estimated policy improvement may be too far off that the decision can be a disaster.

To address this issue, we impose a trust region. We pick the optimal control within this region only. By establishing an upper bound of the potential error, we know how far we can go before we get too optimistic and the potential error can kill us. Within the trust region, we have a reasonable guarantee that the new policy will be better off. Outside the trust region, the bet is off. If we force it, we may land in states that are much worse and destroy the training progress. TRPO and PPO are methods using the trust region concept to improve the convergence of the policy model.
Actor-critic method
Policy Gradient methods use a lot of samples to reach an optimal solution. Every time the policy is updated, we need to resample. Similar to other deep learning methods, it takes many iterations to compute the model. Its convergence is often a major concern. Can we use fewer samples to compute the policy gradient? Can we further reduce the variance of A to make the gradient less volatile?

RL methods are rarely mutually exclusive. We mix different approaches to complement each other. Actor-critic combines the policy gradient with function fitting. In the Actor-critic method, we use the actor to model the policy and the critic to model V. By introduce a critic, we reduce the number of samples to collect for each policy update. We don’t collect all samples until the end of an episode. This Temporal Difference technique also reduces variance.
The algorithm of actor-critic is very similar to the policy gradient method. In step 2 below, we are fitting the V-value function, that is the critic. In step 3, we use TD to calculate A. In step 5, we are updating our policy, the actor.

Guide Policy Search
The actor-critic mixes the value-learning with policy gradient. Again, we can mix Model-based and Policy-based methods together. We use model-based RL to improve a controller and run the controller on a robot to make moves. A controller determines the best action based on the results of the trajectory optimization.
We observe the trajectories and in parallel, we use the generated trajectories to train a policy (the right figure below) using supervised learning.

Why we train a policy when we have a controller? Do they serve the same purpose in predicting the action from a state anyway? That comes to the question of whether the model or the policy is simpler.
Model-based learning can produce pretty accurate trajectories but may generate inconsistent results for areas where the model is complex and not well trained. Its accumulated errors can hurt also. If the policy is simpler, it should be easier to learn and to generalize. We can use supervised learning to eliminate the noise in the model-based trajectories and discover the fundamental rules behind them.

However, policy-gradient is similar to a trial-and-error method with smarter and educated searches. The training usually has a long warm-up period before seeing any actions that make sense.

So we combine both of their strength in the Guided Policy Search. We use model-based RL to guide the search better. Then we use the trajectories to train a policy that can generalize better (if the policy is simpler for the task).
We train both controller and policy in an alternate step. To avoid aggressive changes, we apply the trust region between the controller and the policy again. So the policy and controller are learned in close steps. This helps the training to converge better.

Deep Learning
What is the role of Deep Learning in reinforcement learning? As mentioned before, deep learning is the eye and the ear. We apply CNN to extract features from images and RNN for voices.

A deep network is also a great function approximator. We can use it to approximate any functions we needed in RL. This includes V-value, Q-value, policy, and model.

Partially Observable MDP
For many problems, objects can be temporarily obstructed by others. To construct the state of the environment, we need more than the current image. For a Partially Observable MDP, we construct states from the recent history of images. This can be done by applying RNN to a sequence of images.

Which methods to use?
We have introduced three major groups of RL methods. We can mix and match methods to complement each other and there are many improvements made to each method. Which methods are the best?
This will be impossible to explain within a single section. Each method has its strength and weakness. Model-based RL has the best sample efficiency so far but Model-free RL may have better optimal solutions under the current state of the technology. Sometimes, we can view it more like fashion. What is the best will depend on the year you ask? Research makes progress and out-of-favor methods may have a new lifeline after some improvements. In reality, we mix and match for RL problems. The desired method is strongly restricted by constraints, the context of the task, and the progress of the research. For example, robotic controls strongly favor methods with high sample efficiency. Physical simulations cannot be replaced by computer simulations easily. But yet in some problem domains, we can now bridge the gap or introduce self-learning better. In short, we are still in a highly evolving field and therefore there is no golden guideline yet. We can only say at the current state, what method may be better under the constraints and the context of your task. Stay tuned and we will have more detailed discussions on this.
Thoughts
Deep reinforcement learning is about how we make decisions. In this article, we cover three basic algorithm groups namely, model-based RL, value learning, and policy gradients. This is just a start. How to learn as efficiently as a human remains challenging. The bad news is there is a lot of room to improve for commercial applications. The good news is the problem is so hard but important that don’t expect that the subject is boring. In this article, we explore the basic but hardly touch on its challenge and many innovative solutions that have been proposed. It is one of the hardest areas in AI but probably one of the hardest parts of daily life also. For those who want to explore more, here are the articles detailing different RL areas.
