Dense layers explained in a simple way

A part of series about different types of layers in neural networks

After introducing neural networks and linear layers, and after stating the limitations of linear layers, we introduce here the dense (non-linear) layers.

In general, they have the same formulas as the linear layers wx+b, but the end result is passed through a non-linear function called Activation function.

y = f(w*x + b) //(Learn w, and b, with f linear or non-linear activation function)

The “Deep” in deep-learning comes from the notion of increased complexity resulting by stacking several consecutive (hidden) non-linear layers. Here are some graphs of the most famous activation functions:

List of activation functions, thanks to Sebastian Raschka

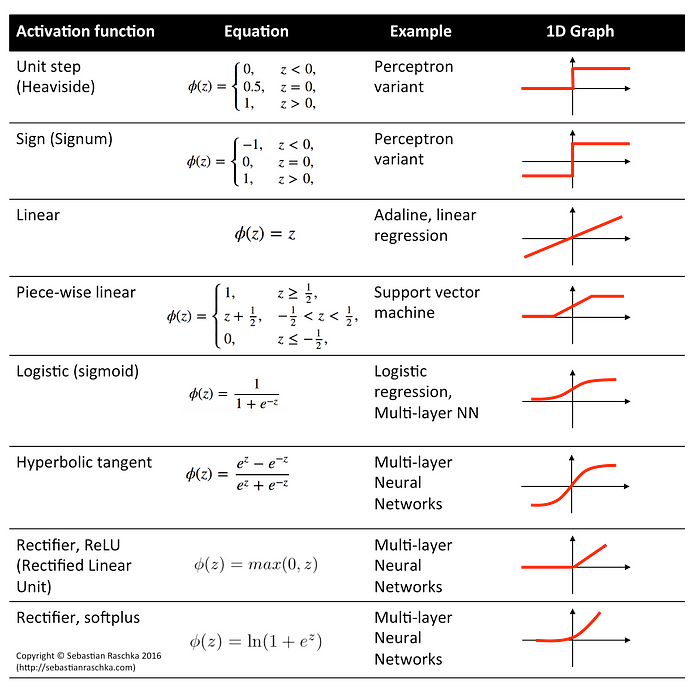
Obviously, we can see now that dense layers can be reduced back to linear layers if we use a linear activation! But then as we proved in the previous blog, stacking linear layers (or here dense layers but with linear activation) will be redundant.

Intuitively, each non linear activation function can be decomposed to Taylor series thus producing a polynomial of a degree higher than 1. By…