AutoLayout Equations and The Trivial Solutions that Magic Away your UIViews

The Lost Socks of Interface Builder

There are times when AutoLayout makes me think of views as socks: sometimes you cannot locate a UIView no matter how simply you laid it out the night before. It doesn’t matter if you did it programmatically or in Interface Builder, it may as well be on the dark side of the moon, or stolen by UIView Gnomes. You suspect Autolayout is the culprit, but you get nothing in the console. Nada. Silent failure. No [UPDATE: Often no] helpful remarks like:

“I’ll assume you know what you’re doing, usually, and were merely distracted by some 18th century disease — say, dysentery — when you gave me illogical and contradictory constraints. By looking or not looking at this window, you are agreeing that it was ok for me to break some of those constraints at my whimsy. Next time, try harder, or don’t try at all, buddy. And stay healthy — cholera is not covered by Apple Care.”

I have begun reading Erica Sadun’s excellent, if only slightly dated*, iOS AutoLayout Demystified. She notes what the Apple Docs say, that autolayout basically solves a system of linear equations. What…??, you ask. This is today’s nugget: you already learned the basics of solving systems of linear equations in high school, if not grade school (for those readers in grade school, read on and learn!).

*“Completely updated for iOS 7 and Xcode 5!”

tl;dr — sometimes the only solution to an equation is the trivial solution (e.g., 1 — x = 1 + x is true when x = 0). This is different than no solution (e.g., x — 1 = x + 1). In autolayout, no solution leads to a warning/crash/constraint-breaking. A trivial solution can often (but not always) lead to silent failure — a view of 0 x 0 dimensions — though in Xcode 7, the compiler has often said “You probably didn’t mean it, I’ll break one of these constraints.”

Appendix

N Equations for N Unknowns

Let’s solve for x, shall we?

x = 3

Have you got it? I hope so. In this equation, there is one unknown, and we can fully solve for the variable, x. The same is true for this variant:

3x — 2 = 7

Although more convoluted, we essentially have a single Unkown, and one equation suffices to solve for it.

If we had two unknowns, however, we would not be able to do so:

y + x = 4

Indeed, the set of possible solutions is infinite, since you can pick any pair of numbers that ‘cancel out’ (for example: [0, 4], [1, 3], [-100, 104], and so on…). That set, by the by, can be represented visually (say, on graph paper) as a Line. But we can solve this:

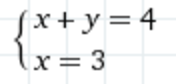
For the visual learners, this would be represented by taking that line (y = -x + 4) and picking the spot where x = 3.

System?

When we presume that the x in the first equation is the very same x in the 2nd equation, we are viewing the two as a system. Put differently, the equations comment on one another. Think of Sudoko.

[caption id=”” align=”aligncenter” width=”300"]

Click Me for something slightly worse![/caption]

Fancy Mathy Pants

In school we learned to “plug in” the variables from one equation into the other in order to solve these (“substitution method”), and most high school math courses teach linear arithmetic (“elimination method”). But there are many sophisticated techniques for solving these equations quickly and efficiently.

[The place to start might be Khan Academy, but I am a big fan of Gilbert Strang’s course (and textbook!), now online for free from MIT (text not free ☹ )].

Conclusion: Solving for x, Solving for UIViews

What about these equations, do they have a viable solution?

x = 3, x = 4

Correct, they don’t! If those equations represented constraints, they would crash the app, or eliminate your views — or Xcode could/might ignore one of them for you, and let you off with a stern warning. And if the latter happens, heed the warning, and fix the constraints — because if you are not deciding how to place your views, who is??